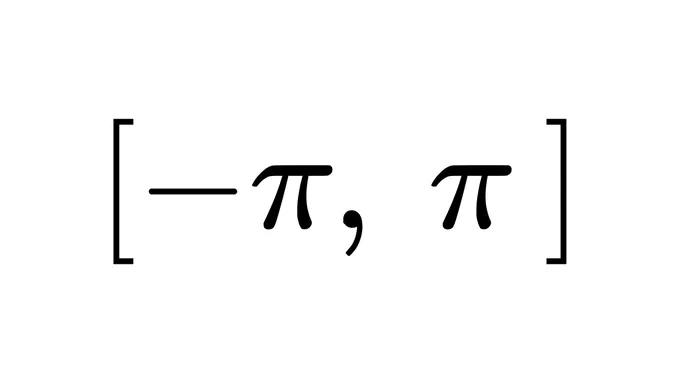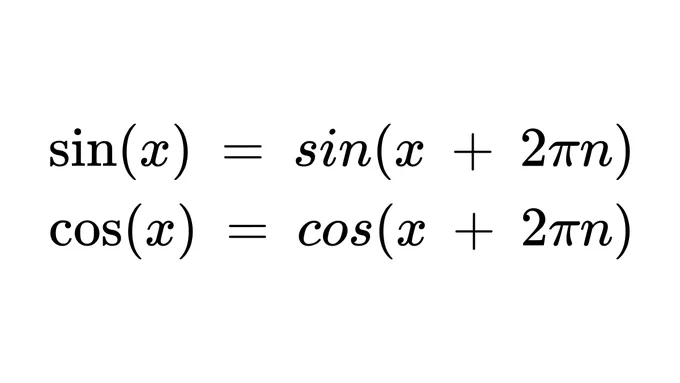let me take you on a sweeping journey into the world of SVG arcs, globs, and the math and geometry behind it — and why they pose an interesting challenge when designing the glob data structure.
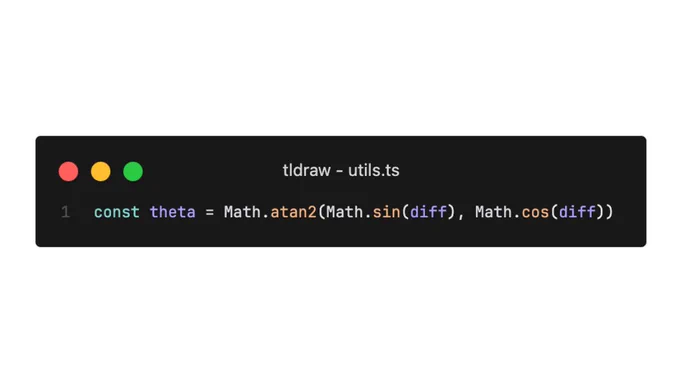
this simple function is key
the caps of a glob are circular arcs, defined by two tangent "end points" found on either the start or end node of the glob.
to draw an SVG arc, we need to define two parameters that result in four different possibilities of which arc to draw.
we can either:
- go clockwise or counter clockwise
- take the larger or smaller arc.
what happens if you hardcode the smaller arc (green) for the left cap? the cap gets "squished" inside its node when we move the handle closer to the circle centre. not good.
how do we fix this?
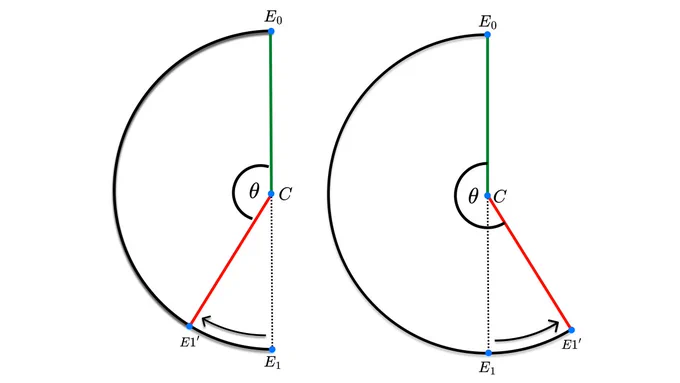
a gotcha with atan2 is that it returns values in the [-180°, 180°] range. so taking two angles returned from atan2 and taking the raw difference can give misleading angles.
you need to normalise them!
Nov 4, 2025 · 11:49 AM UTC
one neat property about the trig functions is that their periodic and thus automatically wrap for you.
you can pass this raw difference to sin and cos and get the correct x, y values on the unit circle, and pass that to atan2.
we can use this angle as a flag to check whether we take the larger or smaller arc.
with atan2 angles > 180° are negative, as they represent clockwise movements and positive when < 180°.
below we switch between the green and red arc as the angles go from ± 180° (or from positive to negative).
problem solved, we get smooth glob caps
this is what I get to do at work and why @tldraw is the best place to be in London right now