๐จ Your RL only improves ๐ฝ๐ฎ๐๐@๐ญ, not ๐ฝ๐ฎ๐๐@๐ธ? ๐จ
Thatโs not a bug โ itโs a ๐ณ๐ฒ๐ฎ๐๐๐ฟ๐ฒ ๐ผ๐ณ ๐๐ต๐ฒ ๐ผ๐ฏ๐ท๐ฒ๐ฐ๐๐ถ๐๐ฒ youโre optimizing.
You get what you optimize for. If you want better pass@k, you need to optimize for pass@k at training time.
๐งต How?
Apr 27, 2025 ยท 4:30 PM UTC
Policy Gradient variants, like PPO, GRPO, all optimize for this objective:
The correctness of each ๐ถ๐ป๐ฑ๐ถ๐๐ถ๐ฑ๐๐ฎ๐น sample ๐บ.
๐ This optimizes for exactly the pass@1 metrics in training time. Training with a pass@1 objective won't probably yield pass@k miracles.โจ
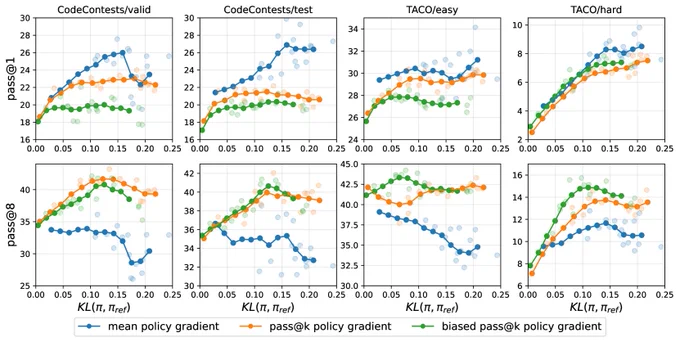
It's a different RL paradigm, in which the reward is not only a function of single trajectory, but a population of trajectories.
Given k samples, pass@k is 1 if at least one of them is correct.
โจ We can define the reward exactly as the maximum of the individual reward.
How does the loss looks like? We derive the following formula for the advantage and contrast that with the pass@1 objective like Dr. GRPO or RLOO.
We observe a ๐ฐ๐น๐ฒ๐ฎ๐ฟ ๐๐ฟ๐ฎ๐ฑ๐ฒ-๐ผ๐ณ๐ณ between pass@1 and pass@k if you train them using different objective:
If you train for pass@1, you get pass@1 increase on eval.
If you train for pass@k, you get pass@k increase on eval.
It's just that simple.
For more details have a look at our preprint in March.
arxiv.org/abs/2503.19595
Joint work with @robinphysics @syhw and ๐ฅ๐ฒ๐บ๐ถ ๐ ๐๐ป๐ผ๐
