🚨 Your RL only improves 𝗽𝗮𝘀𝘀@𝟭, not 𝗽𝗮𝘀𝘀@𝗸? 🚨 That’s not a bug — it’s a 𝗳𝗲𝗮𝘁𝘂𝗿𝗲 𝗼𝗳 𝘁𝗵𝗲 𝗼𝗯𝗷𝗲𝗰𝘁𝗶𝘃𝗲 you’re optimizing. You get what you optimize for. If you want better pass@k, you need to optimize for pass@k at training time. 🧵 How?

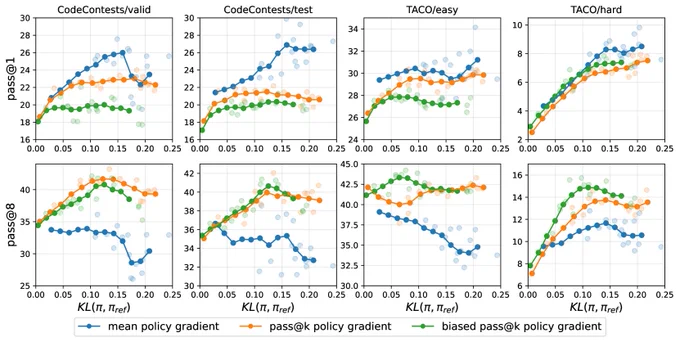
Policy Gradient variants, like PPO, GRPO, all optimize for this objective: The correctness of each 𝗶𝗻𝗱𝗶𝘃𝗶𝗱𝘂𝗮𝗹 sample 𝘺. 👉 This optimizes for exactly the pass@1 metrics in training time. Training with a pass@1 objective won't probably yield pass@k miracles.✨

It's a different RL paradigm, in which the reward is not only a function of single trajectory, but a population of trajectories. Given k samples, pass@k is 1 if at least one of them is correct. ✨ We can define the reward exactly as the maximum of the individual reward.

How does the loss looks like? We derive the following formula for the advantage and contrast that with the pass@1 objective like Dr. GRPO or RLOO.

We observe a 𝗰𝗹𝗲𝗮𝗿 𝘁𝗿𝗮𝗱𝗲-𝗼𝗳𝗳 between pass@1 and pass@k if you train them using different objective: If you train for pass@1, you get pass@1 increase on eval. If you train for pass@k, you get pass@k increase on eval. It's just that simple.