中澤 港%人類生態学者@神戸大学 retweeted
#統計 どういう「工夫」を想定しているかが分からない。
男と女の2分割でも、男と未成年女と成人女の3分割でも、男の割合単独の信頼区間は同じものです。
3分割の場合での複数のパラメータの同時信頼区間(区間の直積型の信頼領域)はそれらとは異なります。
私の方が誤解しているなら教えて下さい。
ハクメス3世 retweeted
‘
おはようございます!!
【難易度:★★★☆☆】
さて問題です。
これは何の支出でしょうか?
<選択肢>
① 外壁・塀等工事費
② 植木・庭手入れ代
③ 火災・地震保険料
正解は本日17時
今日も楽しい一日を!
★ファミマビジョンで出題中★
gate-one.co.jp/news/info/832…
#統計 #クイズ #地理 #GIS
きく retweeted
クイズ:主要国のベンチャーキャピタル投資額 2位の国はどこでしょう?
①日本
②フランス
③イスラエル
④ドイツ
ちなみに、2位の国は対GDP比率でも世界トップクラス。これはほぼ答えに近いかな…?
正解は後ほど、リポストで投稿します。
#地理 #クイズ #地理日めくりクイズ #共通テスト #統計
きく retweeted
‘
おはようございます!!
【難易度:★★★☆☆】
さて問題です。
これは何の支出でしょうか?
<選択肢>
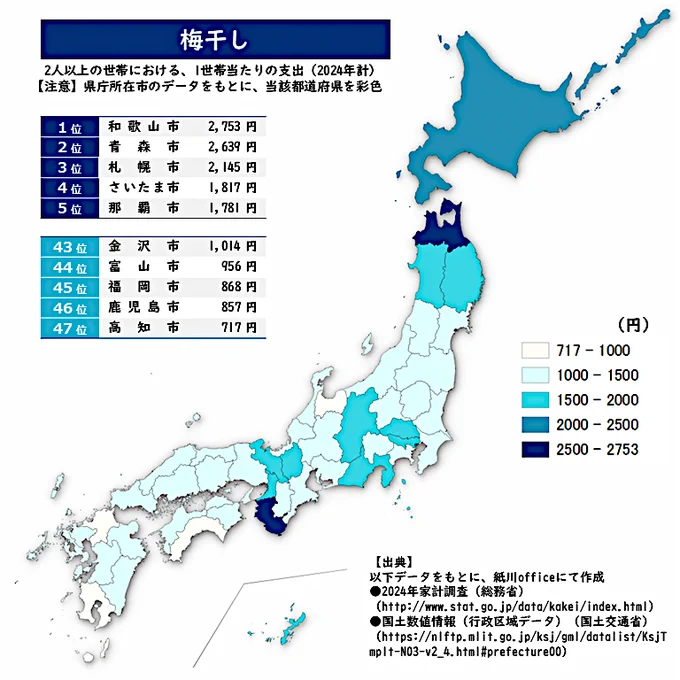
① 干しのり
② 干ししいたけ
③ 梅干し
正解は本日17時にポストします。
今日も楽しい一日を!!
★ファミマビジョンで出題中★
gate-one.co.jp/news/info/832…
#統計 #クイズ #地理 #GIS
#統計 パラメータ(θ, η)の自然な信頼領域を図示すれば、パラメータ(θ, η)のどの値がデータの値と比較的相性が良いかがぱっと見て分かるようになる。
例
↓
#統計 ヒートマップでの色をP値ではなく、S値=-log₂(P値)でつけた場合の
95%信頼領域 = P値≥5%となる(a,p)の値全体
のグラフ。P値=100%とP値=5%に対応するS値はそれぞれ0bitと約4.3bitなのでその間の部分に色がつけられています。
github.com/genkuroki/public/…
#統計 信頼領域として区間の直積型領域を考えることは、対応するP値関数の視点から見ると、十分に自然なものにはなっていないと思う。
目的に合わせて注目するパラメータの個数を2個まで減らして、より自然な信頼領域をグラフで図示するようにした方が良い場合もあると思った。
#統計 (θ₁,…,θᵣ)の区間の直積型95%信頼領域
CR(X)=[L₁(X),U₁(X)]×⋯×[Lᵣ(X),Uᵣ(X)]
のθ₁部分[L₁(X),U₁(X)]は一般にはθ₁の95%信頼区間を与えません。
だから、解説時には、[L₁(X),U₁(X)]をθ₁単独の信頼区間だと絶対に誤解しないように厳しく注意警告しておく必要があると思いました。
#統計 データの値Xに区間を対応させる関数CI₁(X)がパラメータθ₁の95%信頼区間を与えるためには、次が成立している必要があります:
パラメータθ₁のみを値a₁に設定したモデルの確率分布(ただ一つに決まらない)で生成された仮想的なデータXについて、a₁∈CI₁(X)となる確率は95%で近似される。